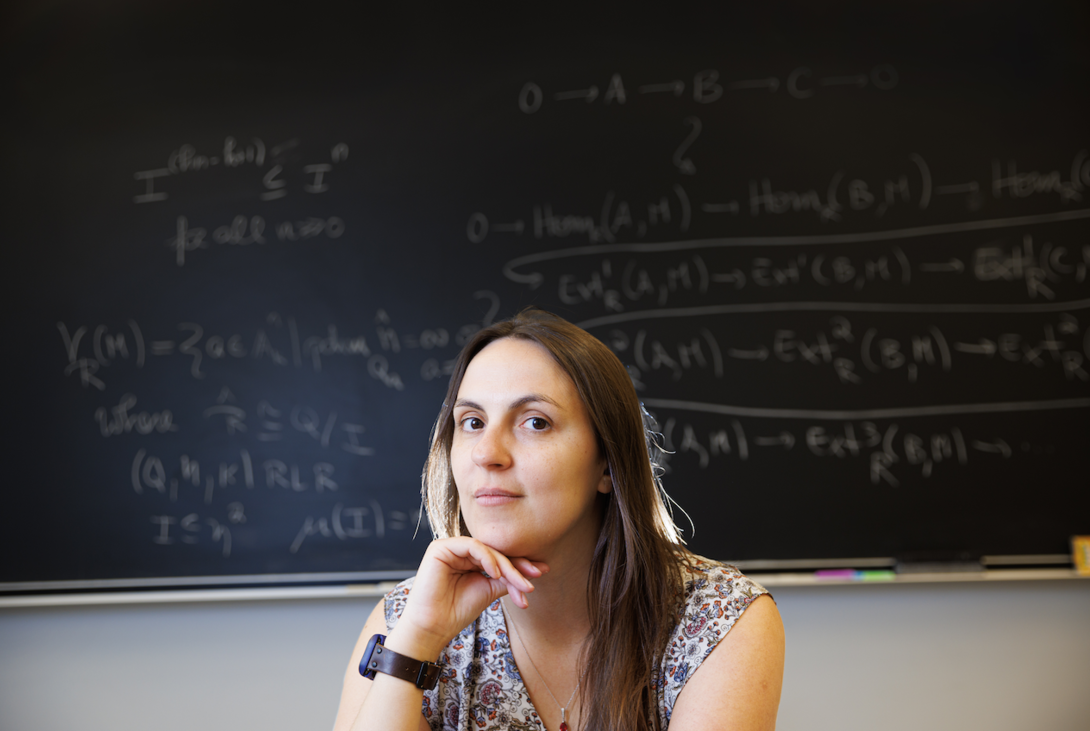
A University of Nebraska–Lincoln mathematician has received a grant from the National Science Foundation to advance her work in commutative algebra, an area of abstract algebra that provides a framework for visualizing and understanding the properties of shapes in higher dimensions that is key to solving real-world problems in robotics, statistics, physics and beyond.

Eloísa Grifo, assistant professor of mathematics, is the first woman from the Nebraska U mathematics department — and the second Husker mathematician overall — to receive funding from NSF’s Faculty Early Career Development Program. With the five-year, $425,000 CAREER grant, Grifo will expand on her work in commutative algebra, particularly as it relates to applications of p-derivations, symbolic powers and cohomological support varieties.

Her work focuses on points of irregularity, called singularities, in the geometric shapes described by a system of polynomial equations. Visually, singularities look like a sharp point, a corner or a crinkle. A circle, represented by the polynomial equation x2 + y2 = 1, has no such points. By contrast, the curvy, V-like shape that results from the equation x2 – y3 = 0 has a singularity, located where the two sides of the V meet.

Grifo is interested in singularities of shapes that are more complex.

“For a 200-dimensional object, I can’t draw it, and you can’t see it, so whatever interesting information I want to extract from it is not something that I can visualize geometrically,” she said.

The solution is to convert the problem from one of geometry to one of algebra: To learn about a shape’s singularities, Grifo probes the algebraic properties of the corresponding equations.

“To us, it’s these points of ‘bad behavior’ that are interesting,” Grifo said. “We want to understand this bad behavior and be able to classify it and distinguish between different types of bad behavior. We want to be able to tell you about the singularities of a 200 or 300D figure.”

The polynomial equation on the left has a solution set that cuts out a circle across the x- and y-axis. With no visual points of “bad behavior,” this solution set has no singularities. The polynomial equation on the right has a singularity at the highlighted corner that crosses the (0,0) point.

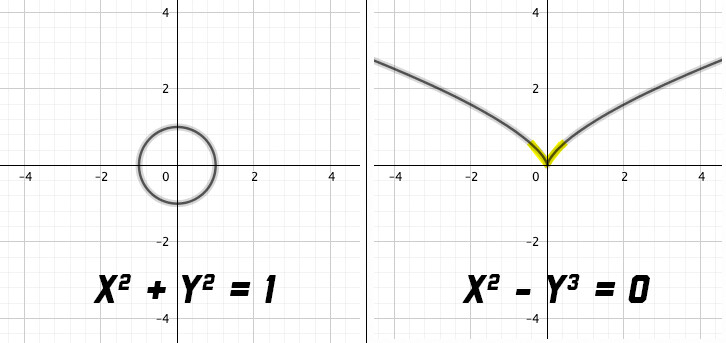
A hallmark of Grifo’s research is importing tools from other fields of mathematics to commutative algebra. She, along with collaborators Jack Jeffries of Nebraska and Alessandro De Stefani of the University of Genova, were the first group to apply a strategy from arithmetic geometry, called p-derivations, to commutative algebra. P-derivations, which stem from the idea of derivatives in calculus, may be a mechanism for solving longstanding questions in commutative algebra.

Grifo also studies higher order interpolation through the lens of symbolic powers, which is an algebraic approach. Interpolation, a classical problem in geometry, involves determining the equations of a curve that pass through a given set of points. Grifo focuses on a variation of this problem: Finding equations with high multiplicity that pass through those points. Multiplicity refers to the number of times a factor appears in a polynomial equation: A very simple example would be that x2 = 0 has a higher multiplicity than x = 0, though both equations are represented by a vertical line on the y axis.

The educational component of Grifo’s CAREER projects aims to engage elementary and middle school students in STEM and mathematics outreach activities. In collaboration with Lincoln Public Schools, Grifo and graduate students will work with students participating in LPS Community Learning Centers, free after-school clubs that amplify the classroom curriculum.

Grifo said the program, called UNL Math Ambassadors, is designed to reach students who are questioning whether math is a viable career pathway. Although Nebraska offers an impressive menu of math outreach activities, such as Math Day and the Nebraska Conference for Undergraduate Women in Mathematics, those programs often engage the best and the brightest — students who are already sold on math.

“I suspect there are students who are not getting the opportunity to participate,” Grifo said. “I think there are kids out there who haven’t had enough opportunities to see how fun and exciting math can be.”

By targeting elementary and middle schoolers, she hopes to reach students before they decide math isn’t for them. She also sees the program as a way to train graduate students to run effective outreach programs. The program will complement the UNL Math Circle initiative, launched by Husker mathematician Jack Jeffries with CAREER funding, which engages high school students.

Grifo will also continue to run the Commutative and Homological Algebra Market Presentations program. It’s an online platform showcasing the work of early career researchers in commutative algebra. She originally launched CHAMPS in 2020 with colleague Keri Sather-Wagstaff of Clemson University to compensate for the lack of in-person conferences during the COVID-19 pandemic. Now, the CHAMPS YouTube channel showcases elevator pitch videos from mathematicians on the academic job market. Grifo hopes the channel increases the job prospects for early-career scholars, particularly those from underrepresented backgrounds.

NSF CAREER awards support pre-tenure faculty who exemplify the role of teacher-scholars through outstanding research, excellent education and the integration of education and research.