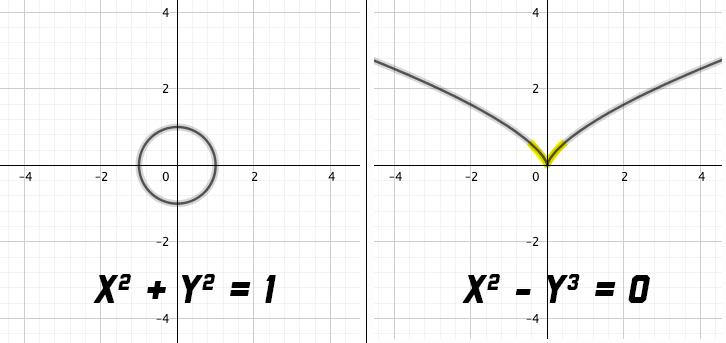A University of Nebraska–Lincoln mathematician has received the department’s first-ever Faculty Early Career Development Program award from the National Science Foundation.
Jack Jeffries, assistant professor of mathematics, will use the $400,000, five-year grant to advance his research in commutative algebra, a field of abstract algebra that, at its heart, is focused on polynomials in many variables. More specifically, he will study singularities — points at which a mathematical object, or geometrical shape, is not “well-behaved” in some way — using differential operators and p-derivations.
“Systems of polynomial equations are ubiquitous throughout the sciences,” Jeffries said. “Singular points are of interest because many standard techniques and algorithms can go haywire at those points.”
Jeffries focuses on the solution sets of polynomial equations, a particular type of algebraic expression involving variables, coefficients and non-negative exponents. Over the most familiar number systems — real numbers and complex numbers — the solution sets to these types of equations can be visualized geometrically via Cartesian coordinates on the x- and y-axis. Each polynomial equation has a solution set that “cuts out” a geometric shape.
Two simple examples would be the polynomial equations x2 + y2 = 1 and x2 – y3 = 0. Each one has a solution set that creates a particular shape. For the first, it would be a circle with a radius of 1 around the origin. For the second, the shape looks a bit like a seagull with its wings spread.
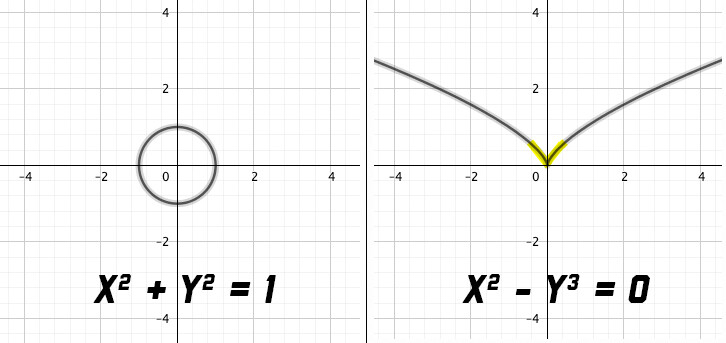
Jeffries is interested in solution sets that have singularities. Visually, these can be thought of as aberrant points in the shape. The circle resulting from x2 + y2 = 1 has no singularities; the seagull of x2 – y3 = 0 does. It’s the corner created at the point of origin.
“Looking closer and closer, the circle starts to look flat,” Jeffries said. “Whereas the shapes cut out by other equations, like x2 – y3 = 0, might have a crinkle, crossing or wrinkle. Geometrically, that’s the idea of a ‘singularity’ in a solution set.”
Jeffries is also interested in looking at polynomial equations and singularities over more exotic number systems. For example, computer data and arithmetic are built on a system of two numbers, zero and one. He aims to develop new tools to study the small-scale behavior of systems of polynomial equations over both familiar number systems and these more exotic systems. More specifically, he will study points of singularity using differential operators and p-derivations, which are extrapolations of the concept of “derivative” in calculus to more general settings. He is looking to establish these methods as tools for better understanding singularities.
Nebraska is considered an international leader in the field of commutative algebra and algebraic geometry. With five faculty and 12 doctoral students focused in the area, the university has one of the nation’s largest research clusters in these fields.
“Jack is a rising young star in the field of commutative algebra,” said Tom Marley, chair of the mathematics department. “His innovative approach to the study of singularities of geometric objects, particularly through his novel use of differential operators, will help keep Nebraska at the forefront of research in commutative algebra and algebraic geometry. We are truly excited that Jack’s work is getting this well-deserved recognition.”
Prior to arriving at Nebraska last year, Jeffries was a faculty member at the Center for Research in Mathematics, known as CIMAT, in Guanajuato, Mexico. As part of his CAREER project’s education component, he aims to advance the relationships he established at CIMAT by hosting faculty from Latin America at the university. Beyond just furthering research collaborations, these visits are intended to expose Nebraska’s graduate students to an international network of mentors and potentially open doors to postdoctoral opportunities.
Jeffries also envisions these Hispanic mathematicians serving as role models for Nebraska’s undergraduate and high school students. One of his goals is to encourage more high school students, particularly members of the Hispanic community, to study mathematics. Toward that end, he will launch a biweekly high school math circle during the academic year. During each session, a university or visiting mathematician will lead students through an activity related to advanced mathematics. To attract Hispanic students, at least one session per semester will be directed in Spanish, and visiting faculty from Latin America will participate as scheduling allows.
Jeffries will make all notes and materials related to the math circle publicly available on a website, enabling anyone across the country to start a similar group.
He’ll also support five graduate students in attending the Pan-American School on Commutative Algebra, a summer school program to be located at the Universidad del Norte in Barranquilla, Colombia; sponsor cross-topical mini-workshops; train graduate students; and continue work on a commutative algebra textbook.
The National Science Foundation’s CAREER award supports pre-tenure faculty who exemplify the role of teacher-scholars through outstanding research, excellent education and the integration of education and research.